
Uma jornada pelo Mediterrâneo
Nossa jornada começa na Cidade de Pisa, região da Toscana, norte da Itália. O ano é 1170, e aqui nascia o lendário Leonardo Fibonacci. Naquela época, os sobrenomes ainda não eram padronizados e o apelido “Fibonacci” foi atribuído a ele muito depois de sua morte, derivado do termo “filius Bonacci”, ou “filho de Bonacci”.
Seu pai era um comerciante italiano e deu a ele uma educação sólida em matemática, para que o ajudasse a lucrar com as rotas comerciais do Mar Mediterrâneo. Ele passou grande parte da vida no norte da África, onde hoje é a Argélia e o Marrocos, onde aprendeu álgebra, geometria e matemática com professores árabes.
Em seu retorno à Europa, publicou sua obra-prima, o “Liber Abaci” (O Livro do Ábaco, ou do Cálculo), no ano 1202, que foi uma revolução no conhecimento. Nesse artigo você vai entender a importância de Fibonacci, e no final eu vou mostrar inclusive como aplicar Fibonacci em investimentos no mercado financeiro.

Os algorismos do Oriente
Um dos impactos mais importantes da obra de Fibonacci foi ter levado para a Europa o sistema numérico indo-arábico que a gente utiliza até hoje, são os dígitos de 0 a 9. Antes disso, os europeus usavam os algarismos romanos, combinações de I, V, X, e mais 4 letras, que eram muito menos eficientes para realizar cálculos (se você mal consegue ler os séculos em algarismos romanos, imagina fazer conta com eles).
Embora Fibonacci não tenha sido amplamente reconhecido na sua época, as suas contribuições para a matemática e a introdução do sistema decimal na Europa foram fundamentais para o desenvolvimento posterior da ciência.

A sequência de Fibonacci
A sequência de Fibonacci é uma série de números em que cada número é a soma dos dois anteriores.
Ou seja:
0+1 = 1.
1+1 = 2.
2+1 = 3
3+2 = 5
e assim por diante, até o infinito. Essa sequência é um importante conceito na teoria matemática.
Ela exibe uma relação de recorrência simples, mas com uma taxa de crescimento exponencial, tendo aplicações em diversas áreas do conhecimento, como na geometria, computação e finanças, como nós vamos ver mais a frente.

A Proporção Áurea
A proporção áurea é a razão que surge quando você divide qualquer número da sequência de Fibonacci pelo número anterior, resultando em aproximadamente 1,618.
Essa propriedade de que números somados com o anterior crescem exponencialmente, e a uma mesma proporção, é a divina proporção e está presente em padrões por todo lado, desde as conchas de moluscos até o crescimento das plantas e de populações, a gente encontra na arquitetura, na música, na anatomia humana e até na espiral das galáxias.
Fibonacci não é uma invenção humana, é uma descoberta. Assim como as leis da física, está escrito no código do universo.

O segmento áureo e as Linhas de Fibo
Qualquer comprimento pode ser dividido de modo que a razão entre a parte menor e a parte maior seja equivalente à razão entre a parte maior e o todo. Essa parte pequena corresponde a 38.2% do todo e a parte maior 61.8%. Sempre que você subtrair 38.2 % de uma unidade vai restar 61,8 e sempre que você subtrair 61.8 vão restar 38.2.
O filósofo Platão disse que as proporções resultantes do segmento áureo é a mais instigante de todas as relações matemáticas, e a considerou como a chave para a física do cosmos. E foi no século XX que os conceitos de Fibonacci foram enxergados nas movimentações dos preços no mercado financeiro.
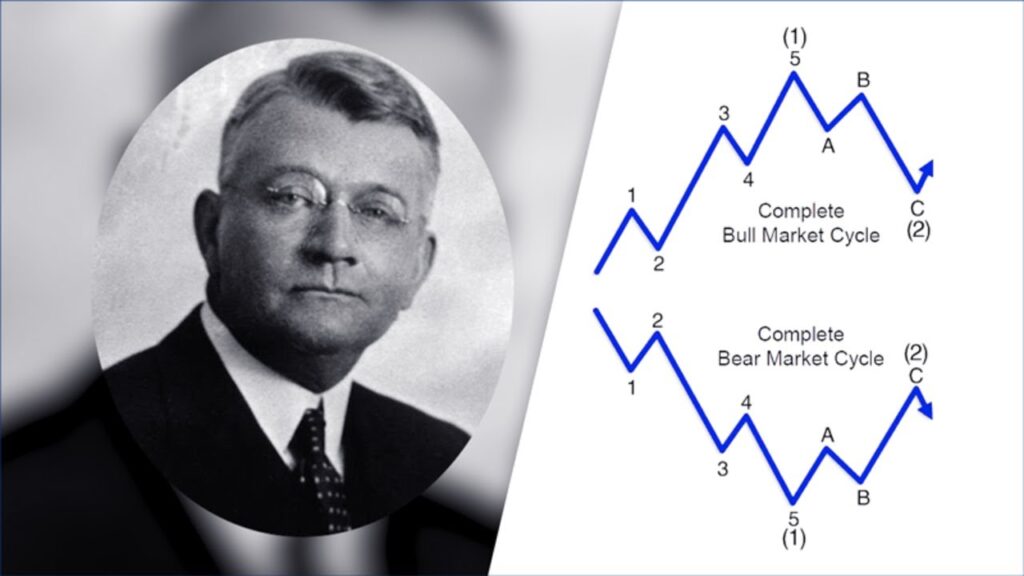
Ressurgimento no Século XX
Um pioneiro na aplicação de Fibonacci às oscilações de preço foi Ralph Nelson Elliott, criador da Teoria das Ondas de Elliott, que observou a presença dessas proporções nos padrões de movimentos de preços.
Outro nome importante é o William D. Gann, um analista de mercado que percebeu a relação entre esses níveis de retração e o preço dos ativos.
Nunca foi tão fácil quanto hoje, aplicar Fibonacci em estratégias de investimentos. Hoje a maioria das plataformas de negociação possuem ferramentas de retração e projeção de Fibonacci.
Assista meu vídeo abaixo para ver na prática como aplicar Fibonacci na Bolsa de Valores (a partir do minuto 4):
>> Veja também:

5 Responses